The Significance of Logarithmic Step Size in Stochastic Gradient Descent Optimization

Efficient optimization in the stochastic gradient descent (SGD) algorithm heavily relies on the selection of an appropriate step size, also known as the learning rate. Various strategies have been introduced to enhance the performance of SGD by manipulating the step size to achieve faster convergence and better results.

The Challenge of Probability Distribution in Step Sizes

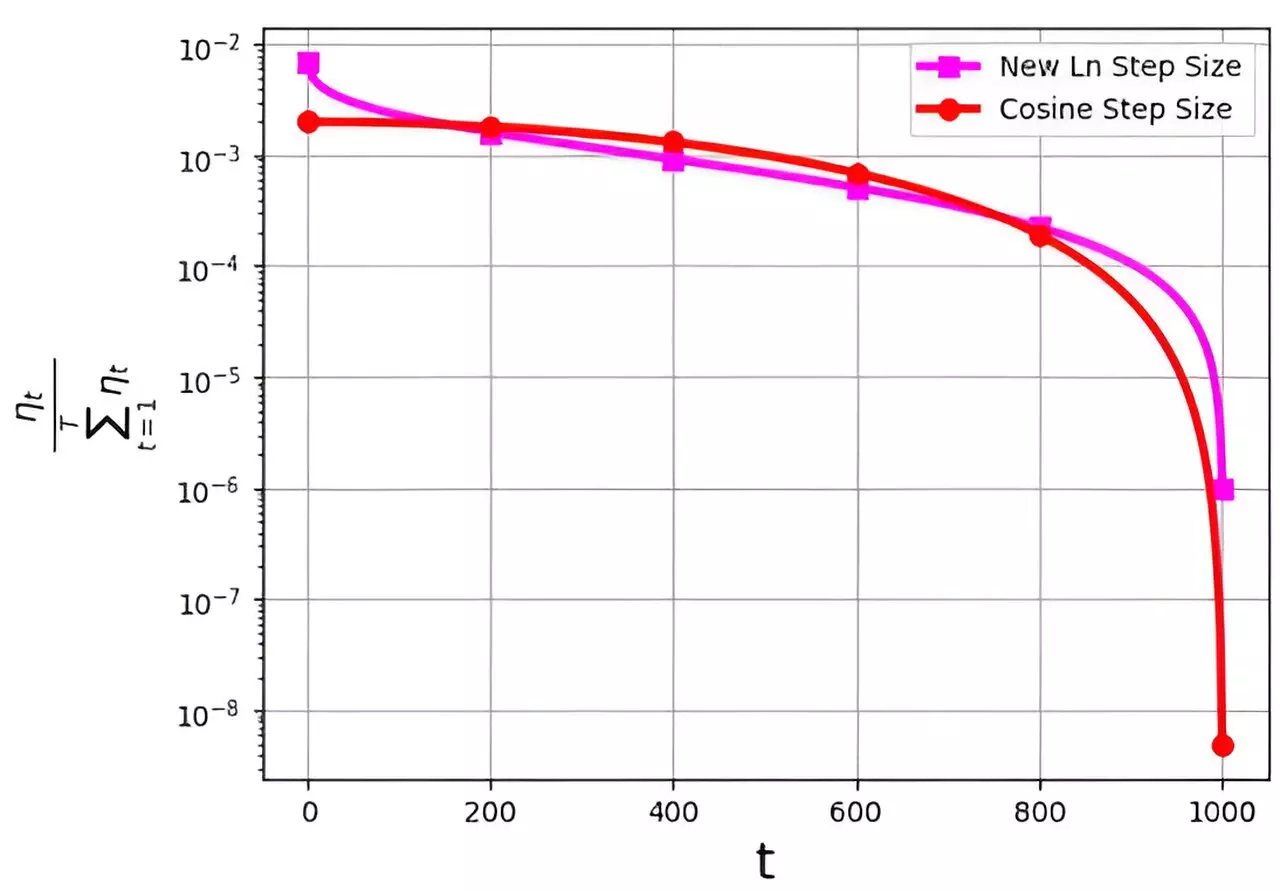
One of the major challenges in implementing different step sizes is the probability distribution associated with them. The distribution of step sizes over the course of iterations, denoted as ηt/ΣTt=1ηt, often faces the issue of assigning extremely small values to the final iterations. This can hinder the effectiveness of the optimization process, especially in the critical concluding stages.

A recent study led by M. Soheil Shamaee, published in Frontiers of Computer Science, introduces a novel approach to tackle the probability distribution challenge in step sizes. The research team proposed a logarithmic step size method for the SGD algorithm, which has shown remarkable improvements in performance, particularly during the final iterations.

The newly proposed logarithmic step size method outperforms the conventional cosine step size method, especially in the crucial concluding stages of optimization. This is attributed to the higher probability of selection for the logarithmic step size during these iterations, leading to better convergence and results.

Numerical experiments conducted on datasets such as FashionMinst, CIFAR10, and CIFAR100 have demonstrated the efficiency and effectiveness of the logarithmic step size approach. The results indicate a significant increase in test accuracy, with a remarkable 0.9% improvement observed in the CIFAR100 dataset when utilizing a convolutional neural network (CNN) model.

The introduction of the logarithmic step size method offers a promising solution to the challenges associated with probability distribution in step sizes for the SGD algorithm. The research findings highlight the importance of optimizing the step size strategy to enhance convergence and performance in machine learning tasks. Further exploration and adoption of the logarithmic step size approach could lead to even more significant advancements in optimization techniques.